Anche quest’anno sono arrivati gli studenti del MIT per fare lezioni di fisica e di matematica in inglese, nelle classi terze, quarte e quinte del liceo. Diamo il benvenuto a Zoe Hinton ed a Mario Contreras, che faranno lezione a Rozzano, ed ad Alyda Huerta, che le svolgerà a Noverasco. Le lezioni sono iniziate il 10 gennaio e termineranno il 27 gennaio.
Tutti gli articoli di luigilombardo
Sulla chiusura o meno delle linee di campo magnetico.
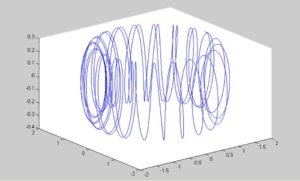
» t=(0:0.01:200)
» x=0.15*sin(0.96*t)+0.15*sin(1.06*t)+1.5*cos(0.05*t)
» y=0.15*cos(0.96*t)-0.15*cos(1.06*t)+1.5*sin(0.05*t)
» z=0.3*cos(1.01*t)
» plot3(x,y,z)
Nella totalità di testi di fisica per il liceo che mi sono capitati tra le mani, nella migliore delle ipotesi, nulla è scritto sulla chiusura o meno delle linee di campo magnetico. Spesso però è scritto che le linee di campo magnetico sono chiuse. In particolare questi testi partono dal teorema di Gauss per il campo magnetico, per affermare che la nullità del flusso implica la chiusura delle linee di campo. Invece implica solo che il numero di linee entranti è uguale a quello delle linee uscenti. Essendomi trovato spesso a discutere sul perché ritengo che le linee di campo magnetico siano aperte, ritengo possa essere utile scrivere qualcosa per giustificare questa mia affermazione. Nei libri di testo, per mostrare la chiusura delle linee di campo, si fa l’esempio del filo percorso da corrente elettrica, di lunghezza infinita e perfettamente rettilineo, oppure della spira, sempre percorsa da corrente, perfettamente circolare e piana. Ma in realtà non esistono né i fili infiniti e rettilinei, né le spire circolari e piane. In questi casi particolari ed ideali le linee sono chiuse, ma nella realtà non è così. Come esempio di un caso più realistico dei due precedenti, possiamo prendere insieme un filo rettilineo, percorso da corrente, ed una spira circolare e piana, sempre percorsa da corrente, il che è come prendere un filo non rettilineo oppure una spira non circolare e piana. Nella figura sono disegnate alcune linee di forza del campo magnetico. Si nota, ma si può anche intuire, che queste linee, pur non avendo inizio e fine, non si chiudono mai, perché nel momento in cui dovrebbero chiudersi, il disturbo, rappresentato dalla seconda sorgente, le devia, impedendone la chiusura. Pertanto le linee continuano all’infinito a riempire lo spazio, ma avendo spessore nullo, la probabilità che possano chiudersi è nulla. A queste mie affermazioni vengono in genere fatte due obiezioni, una matematica ed una fisica. L’obiezione matematica è che le linee, riempiendo tutto lo spazio, si chiudono all’infinito. L’obiezione è inconsistente per due motivi: innanzitutto le linee, pur riempiendo lo spazio, non si chiudono, perché hanno spessore nullo; in secondo luogo le linee sono chiuse al finito, per esempio anche la retta si chiude all’infinito, ma non è una linea chiusa. L’obiezione fisica è che le linee sono relative a grandezze fisiche che sono misurate con una incertezza, pertanto non hanno spessore nullo, ma sono in realtà dei tubicini, che dopo un certo numero di giri finiscono col chiudersi. Anche questa obiezione è inconsistente in quanto le linee di campo non sono grandezze fisiche, ma una rappresentazione matematica di grandezze fisiche, per cui, nonostante l’errore di misura, rimangono linee matematiche con spessore nullo. Buona riflessione. Luigi Lombardo
Il 12 aprile la terza C liceo ha visitato il museo della scienza di Milano
Il 12 aprile la terza C liceo ha visitato il museo della scienza di Milano, con un percorso dedicato a Leonardo da Vinci. Nelle prime due ore si è visitato il museo, sezioni spazio, telecomunicazioni, trasporti. Quindi la visita guidata alla galleria dedicata a Leonardo e di seguito il laboratorio, dove gli studenti hanno sperimentato la tecnica pittorica di Leonardo.
L’esperimento di Eratostene
Dietro invito dello Inspiring Science Education Academy, abbiamo aderito all’iniziativa di ripetere l’esperimento di Eratostene nell’equinozio di primavera, insieme a molte altre scuole sparse nel mondo. All’esperimento hanno partecipato la mia prima C e la prima A con la prof. Salina. L’esperimento consiste nel misurare l’altezza del Sole nel suo punto più alto nel giorno dell’equinozio, e nel confrontare tale misura con quella di un’altra scuola che si trovi sul nostro meridiano, per calcolare la circonferenza terrestre. Abbiamo scelto due scuole di Cagliari, perché Cagliari si trova sul nostro meridiano. Le due scuole sono l’alberghiero Gramsci ed il liceo scientifico Alberti. La misura andava fatta il 21 marzo alle 12:30′:25″, che è l’orario in cui il Sole raggiunge il punto più alto. Purtroppo una dispettosa nuvoletta si è messa davanti al Sole intorno alle 12 e 20 e se ne andata solo alle 12 e 33. Comunque l’errore tra le 12 e 30 e le 12 e 33 è molto piccolo. Il problema principale che abbiamo affrontato è stato l’errore dovuto alla penombra provocata dalle dimensioni non puntiformi del Sole, che abbiamo risolto utilizzando un foro di circa 9 mm posto ad un’altezza di circa 1 metro e misurando la distanza tra la sua immagine e l’ombra di un filo a piombo ad esso legato, come si può vedere dalle immagini. Abbiamo misurato un’ombra di 92,7 +- 0,5 cm per un filo a piombo di 92,3 +- 0,3 cm. Abbiamo ottenuto un’altezza del Sole rispetto all’orizzonte di 44,9 +- 0,2 gradi, corrispondenti ad una latitudine di 45,1 con pari errore, ed un errore rispetto alla vera latitudine dello 0,6%. Questi risultati, confrontati con quelli dell’alberghiero di Cagliari, che ha misurato una latitudine di 38,8, e che si trova a 679,47 km da noi, ci dà una circonferenza terrestre di 38827 km con un errore di 1173 km, più di 1,5 volte l’errore di Eratostene. Misurando invece rispetto ad una ipotetica scuola che si trovi all’equatore, evitando così di cumulare i nostri errori con quelli dell’altra scuola, abbiamo un errore di soli 245 km.
Luigi Lombardo
Terminato, per quest’anno, il progetto GTL

Venerdì 29 gennaio è stato l’ultimo giorno di lezione con Ben.
Nonostante l’argomento, la relatività ristretta, sia indubbiamente difficile e Ben l’abbia trattato a livello quasi universitario, in particolare riguardo al formalismo matematico, e l’uso della lingua inglese, anzi americana, il test di verifica, a risposta multipla, ha dato un risultato medio di circa lo 85% di risposte giuste, sia nella sede di Rozzano sia in quella di Noverasco. Seguirà una verifica con le modalità a noi usuali ed in italiano, ma il risultato del test in inglese è sicuramente positivo.
Questo dovuto principalmente alle capacità didattiche di Ben, che ha parlato lentamente e scandendo le parole, ed ha spiegato con chiarezza, scrivendo i punti salienti sulla lavagna. Non essendo scontato che lo studente che il MIT ci assegna abbia le capacità di Ben, mi sento di poter dire che abbiamo avuto anche un po’ di fortuna, che non guasta mai. Per sintetizzare il giudizio di noi insegnanti su Ben, posso riportare quanto abbiamo scritto nel bigliettino di saluti e di ringraziamento:
“Dear Ben,
it was a pleasure to work with you. We did appreciate your competence, hard working, clear speaking, didactical ability, helpfulness, patience with our bad English, and congeniality. Thank you very much.”
Luigi Lombardo
Corsi di fisica in collaborazione col MIT

Lunedì 11 gennaio sono iniziate le lezioni di Ben Harpt, uno studente del secondo anno del MIT, e termineranno il 29 gennaio.
Le lezioni riguardano la relatività ristretta e sono rivolte alle quinte liceo, sia di Noverasco sia di Rozzano, e dureranno tutto il mese di gennaio. Le lezioni sono ovviamente in inglese perché Ben non conosce l’italiano.
Il progetto si chiama GTL (Global Teaching Lab) ed è organizzato in collaborazione col MIT di Boston, e coordinato dal Pacioli di Crema, che è scuola capofila del progetto.
Il referente, Luigi Lombardo



